Jared Barber, Ph.D.
Associate Professor, Mathematical Sciences

Associate Professor, Mathematical Sciences
See all publications:
Movie of a migrating cell. Migrating cells play important roles in many scenarios including during wound healing, embryo development, cancer cell metastasis, and vessel growth (angiogenesis). Better characterizing what happens as they migrate will help us learn how to speed up or slow down cells and improve patient outcomes. (Xu, Barber, Zhu, SMB 2025)
Movie of a two-dimensional osteocyte (bone cell) embedded in bone and subject to external forces. (Barber, SMB 2023)
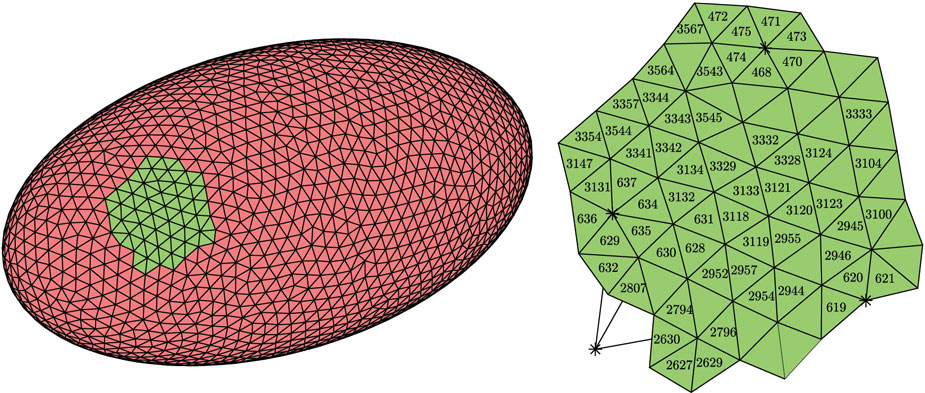
Discretization of an ellipsoidal biological cell into an interconnected network of damped springs representing the cell membrane and cytoskeleton. Such models can be used to determine how forces on cells like osteocytes (bone cells) can cause cells to release signals that affect bone growth.
(Albert et al., submitted 2023)
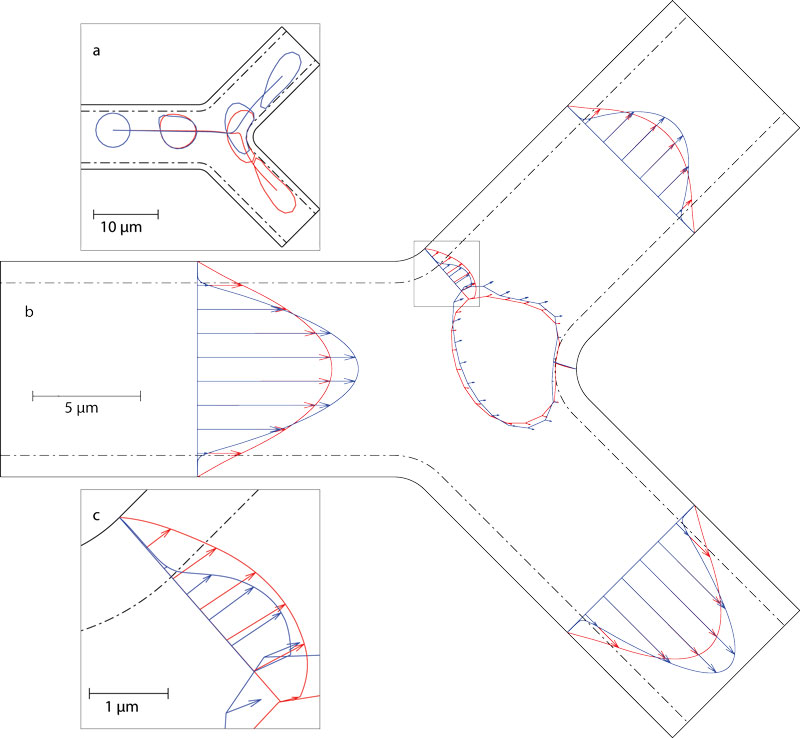
Model of red blood cell passing through a capillary bifurcation lined with a protein coating called the endothelial surface layer. Determining red blood cell distributions using models like these can help determine distributions of other important quantities like the oxygen carried by the red blood cells.
(Triebold and Barber, 2022)
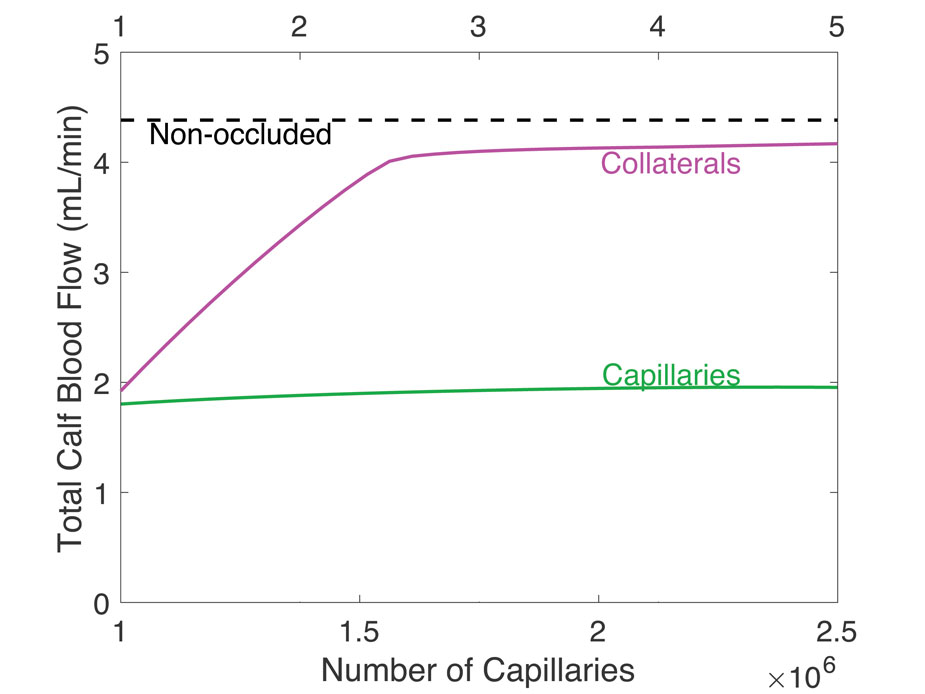
How increased numbers of capillaries and increased number of collateral vessels (carry flow around a clot) affect blood flow. Adding collateral vessels increases flow more suggesting doctors target increasing number of collaterals instead of number of capillaries in order to improve flow after a blood clot.
(E Zhao, J Barber, M Burch, J Unthank, J Arciero, 2020)
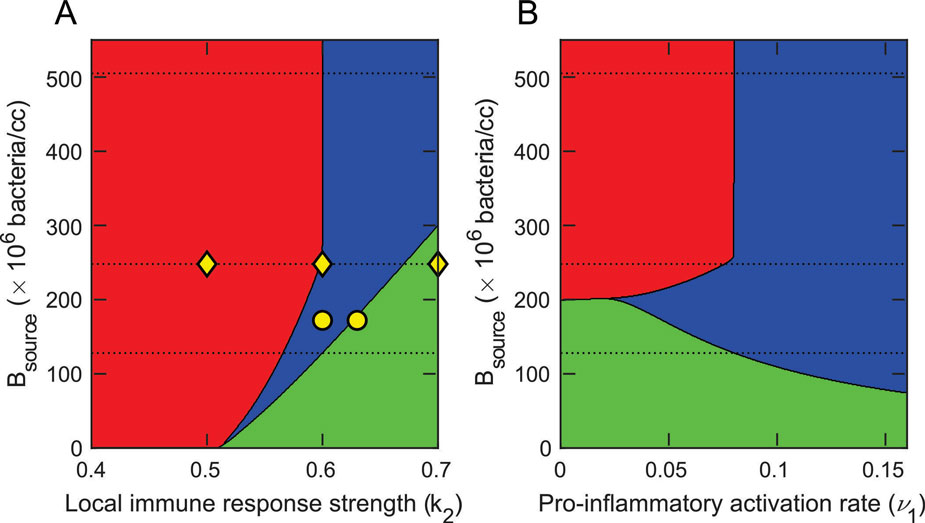
Regions of death in rats due to being overwhelmed by bacteria (red) and the immune response (blue). Surviving animals lie in the green region and Bsource is the amount of bacteria originally injected into the animals. Knowing what parameters we can try to change to improve patient outcomes during bacterial infections (aka sepsis) is very helpful.
(J Barber, A Torsey, A Carpenter, Y Vodovotz, R Namas, J Arciero, 2019)